十大排序算法之归并排序、快速排序、堆排序

归并排序

介绍

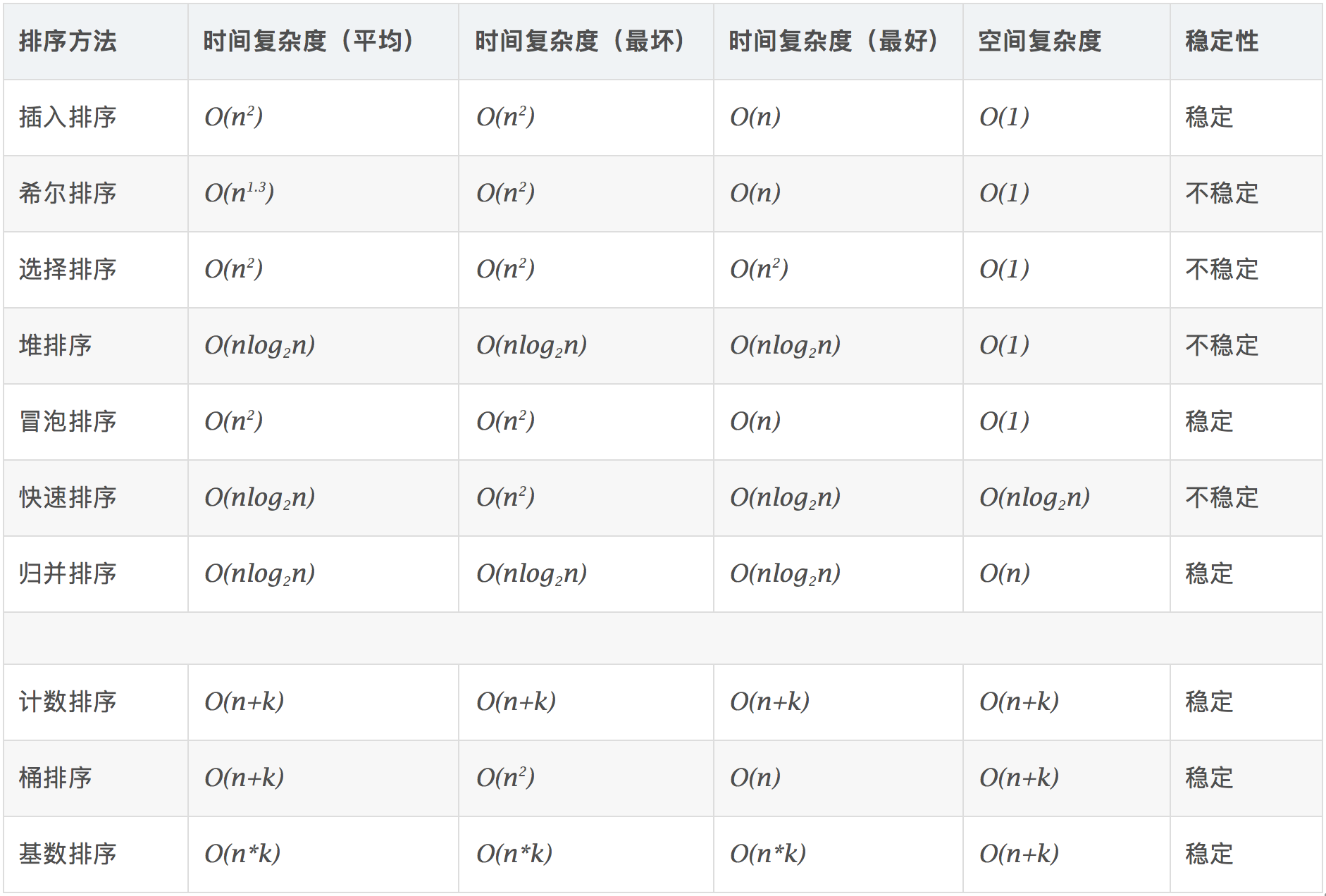
归并排序 $(Merge-sort)$ 是利用归并的思想实现的排序方法，该算法采用经典的分治 $(divide-and-conquer)$ 策略。

如图，具体来说，归并排序在排序的时候，会把一段数组拆分成不同的小数组（临界时只有一个元素），并在合并时排序。

复杂度/稳定性

时间复杂度

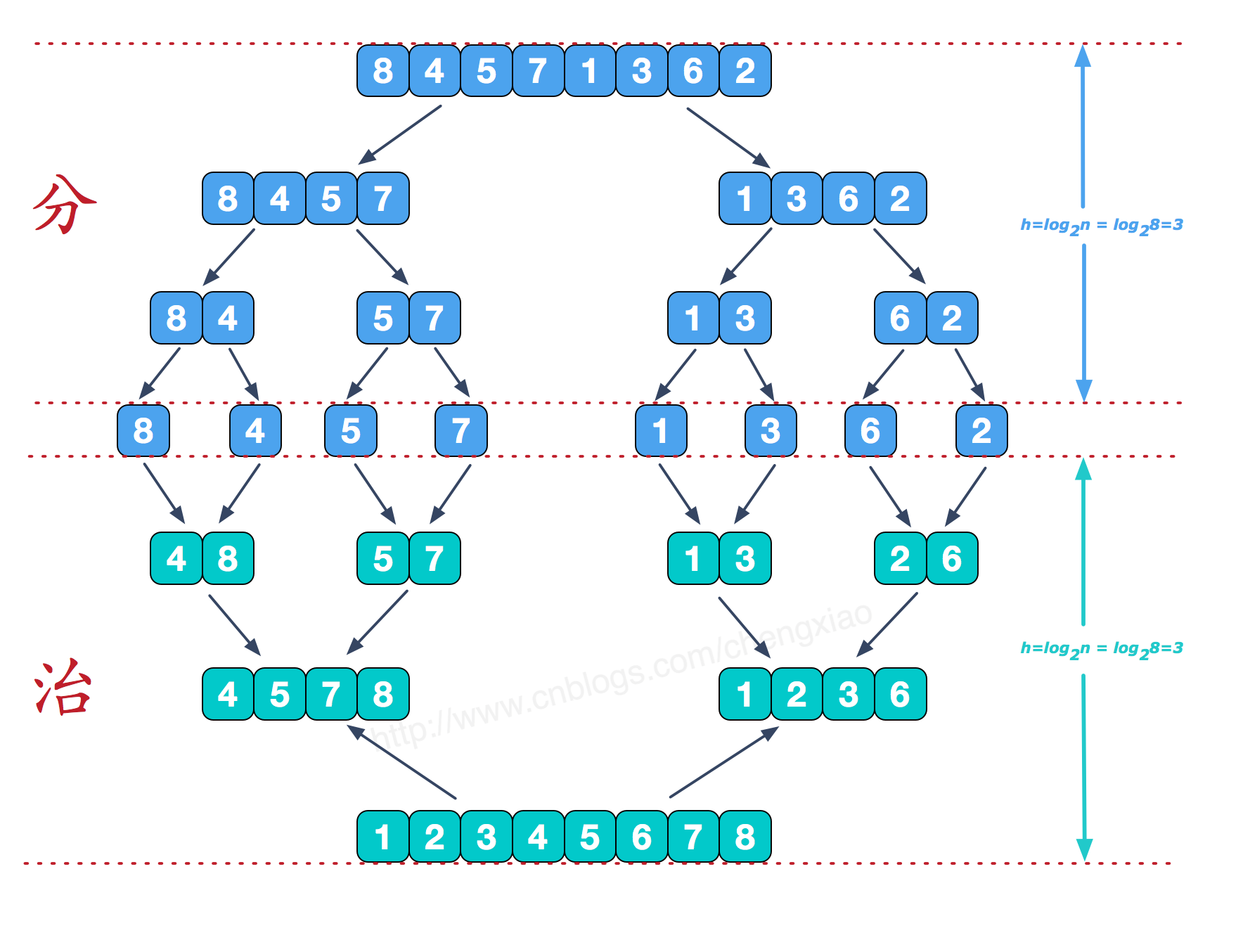
以上图代码为例，此时 $n = 8$ ，可以看到，归并排序的分段是以下标二分的办法.

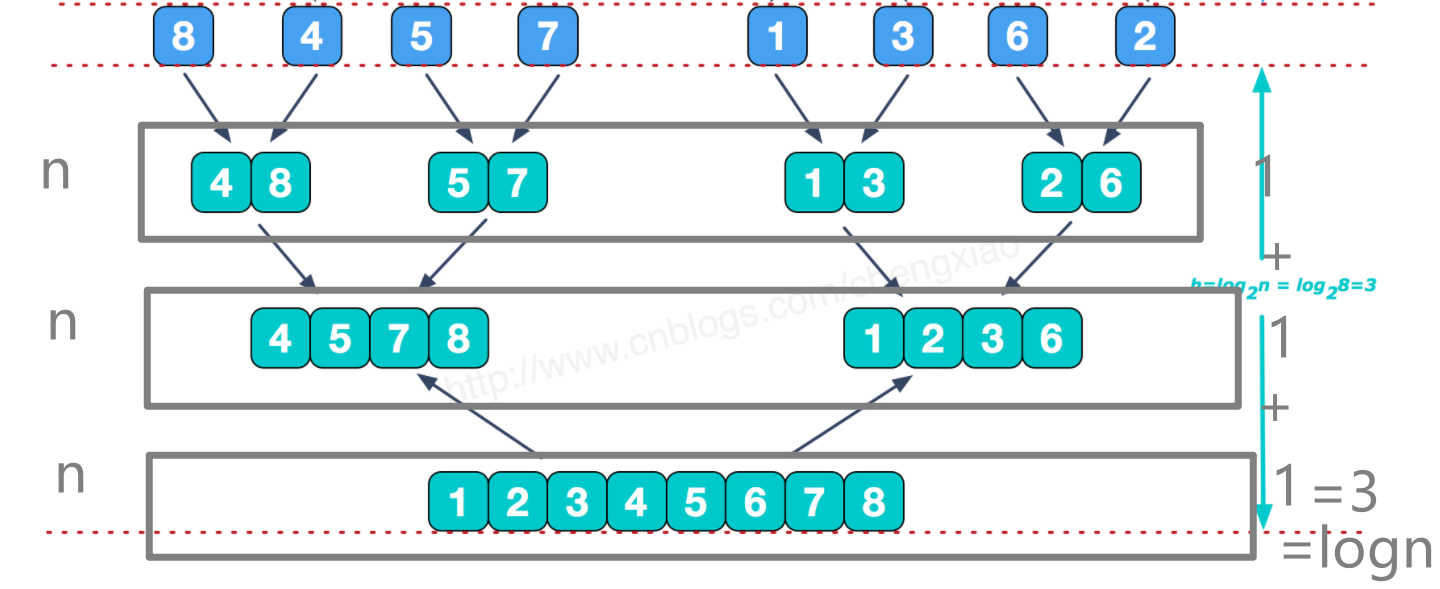
如下图，具体来看，对于分出的每两段数组合并的时候，每一层都会比较 $n$ 次，总共有 $log_2n$ 层，时间复杂度为 $O(nlog_2n)$

稳定性

每两段数组都是相邻的，相同的数合并时相对位置不会变化，因此它是稳定的。

代码实现

以下是c++实现，请参考注释理解：

const int N = 1e4+5;
int n, tmp[N], a[N];
void fsort(int l, int r){
    //先进行递归分组
    if(l >= r) return ;//临界情况，分得的数组最小为1
    int mid = (l+r)/2; //取中间值
    fsort(l, mid); //左边
    fsort(mid+1, r); //右边

    //回溯时进行合并，并排序，因为不能直接在原数组操作（），所以新定义tmp数组暂存合并结果
    int i = l, j = mid+1, k = l;
    while(i <= mid && j <= r){ //比较两个序列每个元素的大小并按次序存入暂存数组
        if(a[i] <= a[j]){
            tmp[k] = a[i];//左边区间的数小，放入
            i++;
            k++;
        }
        else{
            tmp[k] = a[j];//右边区间的数小，放入
            j++;
            k++;
        }
    }
    //还有可能其中一个数组有多出来的数，需要额外放置
    while(i<=mid){
        tmp[k]=a[i];
        i++;
        k++;
    }
    while(j<=r){
        tmp[k]=a[j];
        j++;
        k++;
    }
    //把暂存区的数存入原数组
    for(int i = l; i <= r; i++)
        a[i] = tmp[i];  
}
signed main(){
    fsort(1, n);
    return 0;
}

快速排序

介绍

快速排序 $(Quick-sort)$ 利用二分思想，完成数列的排序操作。

快速排序通过在待排序序列中选取基准值，再将数列调整为以基准值位置为界，一侧比基准值小，另一侧则比基准值大，然后递归两侧执行同样操作，即可完成排序。

如图1：

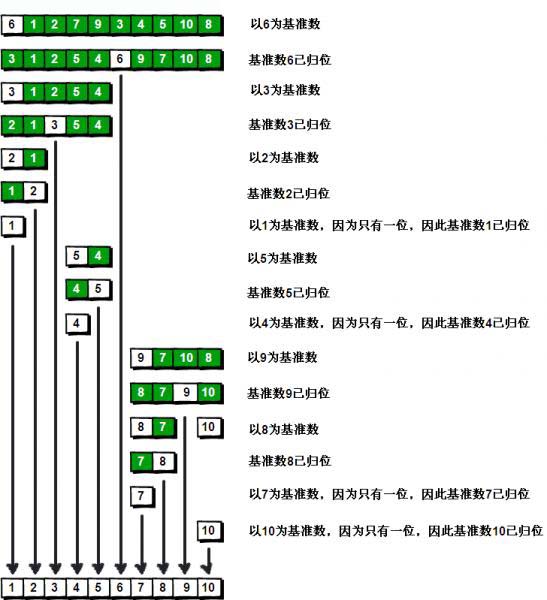
而具体到每次操作，可以参考下面这张图2：

复杂度/稳定性分析

时间复杂度

$\qquad$ 最好情况下，每次划分可以均衡，类比归并排序，每一层排 $n$ 个数，共有 $log_2n$ 层，时间复杂度为 $O(nlog_2n)$

$\qquad$ 最坏情况下：基准值选取最值，每次划分会出现空序列，需要划分 $n$ 次，即共有 $n$ 层，时间复杂度为 $O(n^2)$

同理，如果基准值失去随机性，快速排序的时间复杂度也会退化到 $O(n^2)$

稳定性

快速排序每次按照基准值分类的时候，如上图，若两个元素数值相等，在 $i$ 、 $j$ 互换的过程中，相对位置会发生变化，所以不稳定。

代码实现

以下是c++实现，请参考注释理解：

const int N = 1e4+5;
int n, a[N];
void quicksort(int l, int r){//参考上图2理解
    if(l >= r) return ;//不要越界
    int t = a[l]; //选基准值，如上图，选第一个位置的
    int i = l, j = r;
    while(i < j){ //i!=j时，进入循环
        while( a[j] > t ) j--; //从后往前依次寻找比基准值小的
        while( a[i] <= t && i<j) i++;//从前往后依次寻找比基准值大的
        if(i < j) swap(a[i], a[j]);//满足i < j才能交换，不能相同位置互换
    }
    swap(a[l],a[i]); //把基准值放到合适的位置，此时i = j
    quicksort(l,i-1);//继续向下分
    quicksort(i+1,r);
}
signed main(){
    quicksort(1, n);
    return 0;
}

堆排序

堆排序 $(Heap-sort)$ 是借助堆这种数据结构完成的排序，思路类似于选择排序。

它和选择排序最大的不同是使用了树这一数据结构，把选择排序效率低下的一个个元素遍历的查找改为在树中查找。

前置芝士：堆

如图，堆是一种特殊的完全二叉树，分为大顶堆与小顶堆两种：

1. 大顶堆： 完全二叉树中任一非叶子结点的值都大于等于其子结点的值。
2. 小顶堆： 完全二叉树中任一非叶子结点的值都小于等于其子结点的值。

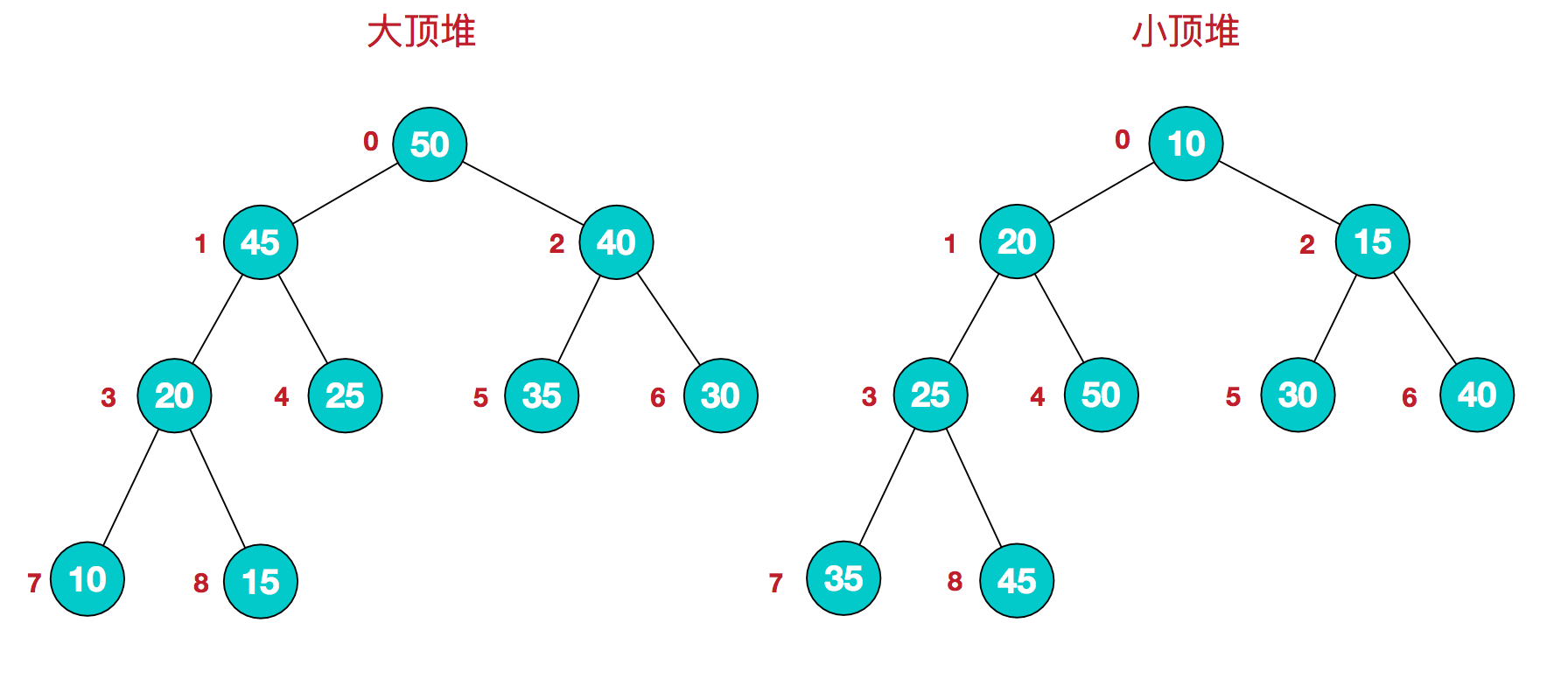
介绍

选择排序的原理还是很好懂的，所以跳过这一块（类比即可），着重讲如何用堆查找元素。

如果我们需要数组元素单调递减，需要最终形成一个大顶堆：从下往上倒序遍历非叶子结点（没有儿子节点的节点），通过交换方式依次调整父子结点顺序，直至符合大顶堆的规则。

举例：有如图的一个数组，需要这样操作便可得到一个有序的数组。

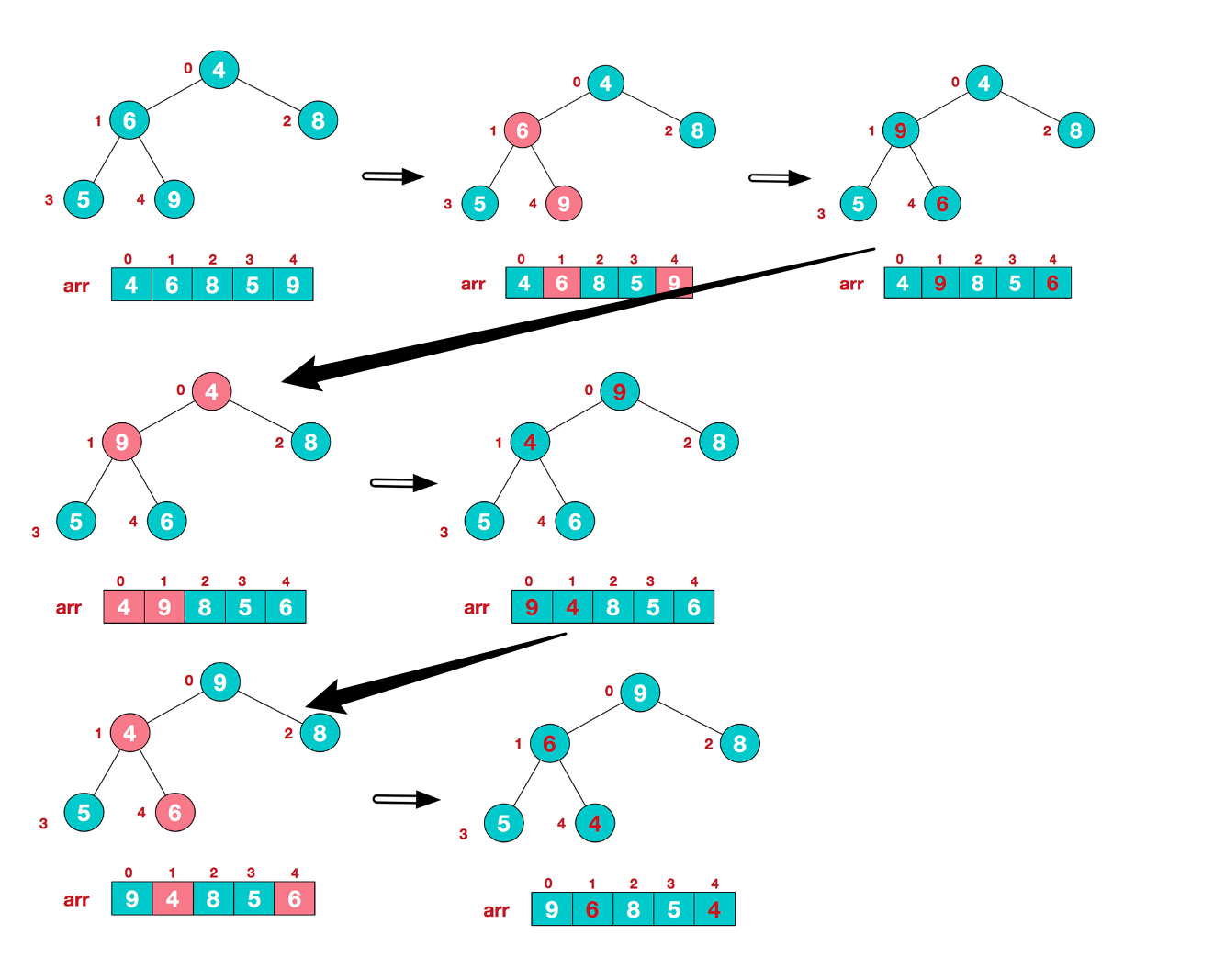
复杂度/稳定性分析

时间复杂度

和选择排序类似，总共需要操作 $n$ 个数，不同的是，选择排序操作一个数需要 $n$ ，而堆排序查找一个数只需要 $log_2n$ ，所以堆排序的时间复杂度是 $O(nlog_2n)$

稳定性

堆排序和选择排序类似，排序过程中相同元素位置发生改变，不稳定。

代码实现

以下是c++实现，请参考注释理解：

const int N = 1e4+5;
int m, a[N]
//堆排序
//堆部分
void adjust(int i, int parent)
{
  int child = parent * 2;//先判断儿子
  // 保证判断的范围不超过i
  if(child + 1 <= i && a[child] < a[child + 1]){
    child++;//选择两个儿子中较大的那个往上传递（维护大顶堆）
  }
  if(a[child] > a[parent]){
    swap(a[child], a[parent]);//如果儿子比较大，就往上交换
    if(child <= i / 2){//不超过i的父节点
      adjust(i, child);//如果当前节点更新，那么当前节点的子节点也需要更新
    }
  }
}
//主体排序部分
void heapSort(){
  for(int i = n; i > 1; i--){//从右侧往左侧维护，注意不能从左往右，因为不能保证其子节点已经被维护过
    for(int j = i / 2; j >= 1; j--){	//从i节点的父节点开始维护
      adjust(i, j);	//以j号节点往根节点调整，传递的i辅助判断是否越界
    }
    swap(a[1], a[i]);//此时树根是下标[1, i]范围内最大的数，和当前位置交换（参考选择排序）
  }
}
signed main(){
    heapSort();
    return 0;
}